A Quick and Dirty Words With Friends Solver: Part 1
It's not cheating it's science
We've all been there. You're 50 points and two games down on words with friends. The pain and humiliation is beginning to get very real. If you don't turn this around you will probably have to change your name and go live in a forest somewhere. It's crunch time.
Whilst most normal people would just accept defeat and spend a couple of days nursing a bruised ego, I simply could not. Instead, I spent those two days building this: a words with friends solver in Python. Ha! Who's a loser now!
For those that don't know, words with friends is essentially budget/american scrabble. I've recently found myself playing tonne of games on the facebook messenger app and I have to say it's both very fun and very addictive. But it got me thinking. How easy would it be for a computer to comprehensively search through every single permutation of possible letter placements and find the highest scoring word? The total number of possibilities when it comes to combinations and permutations gets out of hand very quickly, with pesky factorials popping up all over the shop, but I hoped that with just seven letters on an 11x11 board the numbers would stay manageable. And I'm happy to say that for the most part, they do! In fact, the solver is more or less instanteneous.
If you just want to beat your mates and aren't interested in how it's done, head over to the github repo , clone it and follow the instructions in the README:).
So. How is it done?
I'm going to break this down into two posts. The first will just set up the basic mechanics of the board and take a quick look at how to start building a solver. The second will go in depth on how to find the best solution for a given board.
1.1 The WWF Dictionary
The first thing to note is that the WWF dictionary is based off of 'ENABLE', which is a specific set of words. It also has some naughty words removed and some modern words added. Unfortunately the company doesn't tell you ecactly which words are included but
this post
does a bit of detective work to try and work it out. Using that, I was able to create what I believe is a
pretty
accurate WWF dictionary and save it to the file
dictionary.txt
which you can download from the repo. As you might imagine, the code involves searching through this dictionary a lot, so the first thing I wanted to do is sort this dictionary into (confusingly) a python dictionary, with 27^3 (because we include a blank letter in case the word is less than three letters long) keys, which are the first three letters of a word. That way, if we want to know whether 'splines' is actually a word we only have to search through the set of words beginning with 'spl', which is much faster.
with open('dictionary.txt', 'r') as f:
dictionary = f.read().splitlines()
def sort_dict():
'''A function to sort the dictionary by the first
three letters of each word'''
sorted_dict = {}
alphabet = 'abcdefghijklmnopqrstuvwxyz '
for letter1 in alphabet:
for letter2 in alphabet:
for letter3 in alphabet:
sorted_dict[letter1 + letter2 + letter3] = []
for word in dictionary:
starting_letters = word[:3]
l = len(starting_letters)
if l == 3:
sorted_dict[starting_letters].append(word)
elif l == 2:
sorted_dict[starting_letters + ' '].append(word)
elif l == 1:
sorted_dict[starting_letters + ' '].append(word)
return sorted_dict
sorted_dict = sort_dict()
The next step is to build a function that queries whether a word is in the dictionary or not, which is pretty simple.
def exists(word):
'''Find out whether a word is in the dictionary'''
starting_letters = word[:3]
l = len(starting_letters)
if l == 3:
return word in sorted_dict[starting_letters]
elif l == 2:
return word in sorted_dict[starting_letters + ' ']
elif l == 1:
return word in sorted_dict[starting_letters + ' ']
1.2 The Board Set-up
The next thing to do is to set up the dimensions and mechanics of the words with friends board. Below is a picture of an empty board.
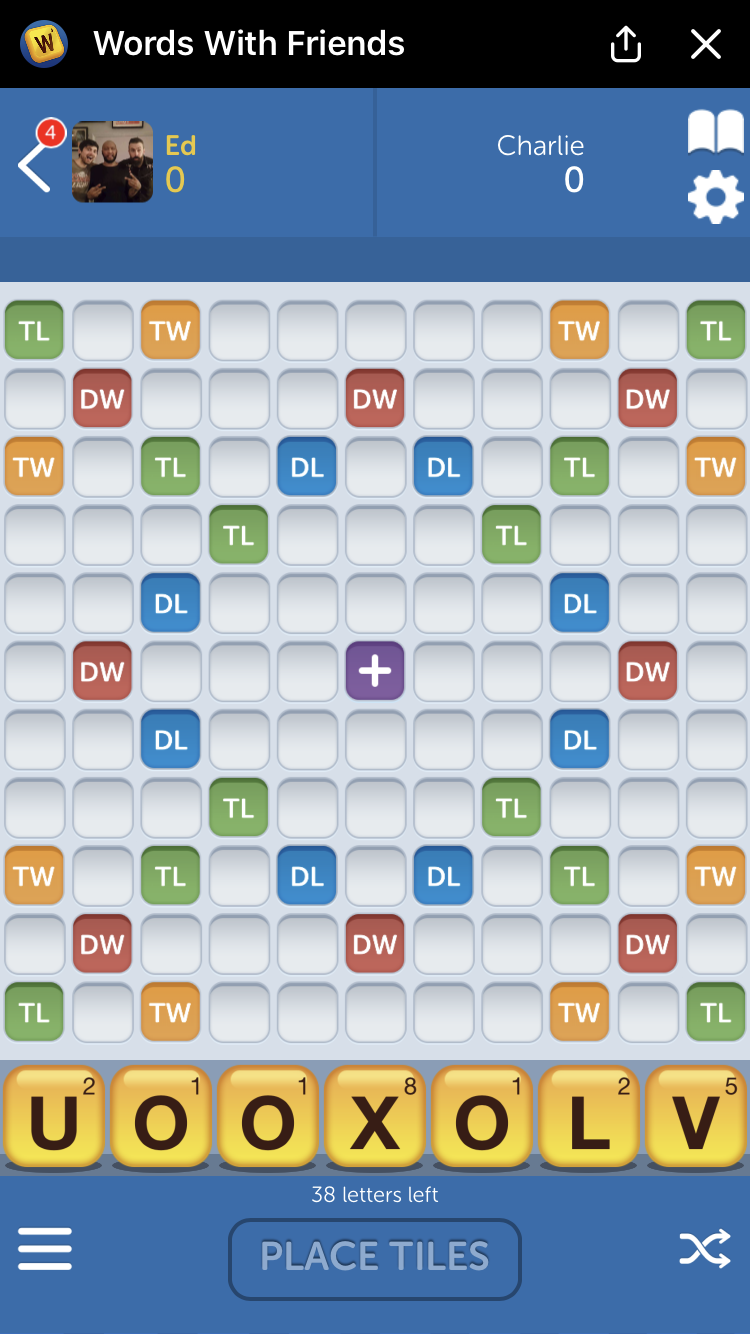
We can specify the (x, y) coordinates (from 0 to 10) of each of the four differennt power-ups and also the number of points each letter is worth.
# double letter coordinates
dls = [(2, 4), (2, 6), (4, 2), (4, 8),
(6, 2), (6, 8), (8, 4), (8, 6)]
# triple letter coordinates
tls = [(0, 0), (2, 2), (3, 3), (7, 7), (8, 8), (10, 10),
(0, 10), (2, 8), (3, 7), (10, 0), (8, 2), (7, 3)]
# double word coordinates
dws = [(1, 1), (9, 9), (1, 5), (1, 9),
(5, 9), (5, 1), (9, 1), (1, 5), (9, 5)]
# triple word coordinates
tws = [(0, 2), (0, 8), (2, 10), (8, 10),
(2, 0), (8, 0), (10, 2), (10, 8)]
# letter values
points = {'a': 1, 'b': 4, 'c': 4, 'd': 2, 'e': 1,
'f': 4, 'g': 3, 'h': 3, 'i': 1, 'j': 10,
'k': 5, 'l': 2, 'm': 4, 'n': 2, 'o': 1,
'p': 4, 'q': 10, 'r': 1, 's': 1, 't': 1,
'u': 2, 'v': 5, 'w': 4, 'x': 8, 'y': 3,
'z': 10}
The next task is to creat a
Board
class that holds information about the board. The
__init__
method creates two key vairables. Namely
letters
and
powers
. These are NumPy character arrays that hold the letters currently on the board, and the unactivated power-ups. The reason I choose to use a NumPy array as opposed to just a set of lists is it makes slicing and indexing a little more natural, making it easier to extract a specific row or column.
import numpy as np
class Board:
def __init__(self):
self.letters = np.chararray((11, 11), itemsize=1, unicode=True)
self.powers = np.chararray((11, 11), itemsize=3, unicode=True)
for x in range(11):
for y in range(11):
if (x, y) in dls:
power = 'dlr'
elif (x, y) in tls:
power = 'tlr'
elif (x, y) in dws:
power = 'dwr'
elif (x, y) in tws:
power = 'twr'
else:
power = ''
self.letters[x, y] = ''
self.powers[x, y] = power
In order to make it quick and easy to edit letters on the a board and get a solutinon out, I need a function that ingests a string representation of the board, adding it the class variable. The board string needs to be of the form:
board_string = '''
A B C D E F G H I J K
--------------------------------------------
| | | | | | | | | | | | 1
--------------------------------------------
| | | | | | | | | | | | 2
--------------------------------------------
| | | | | | | | | | | | 3
--------------------------------------------
| | | | | | | | | | | | 4
--------------------------------------------
| | | | | | | | | | | | 5
--------------------------------------------
| | | | | | w | o | r | d | s | | 6
--------------------------------------------
| | | | | | | | | | | | 7
--------------------------------------------
| | | | | | | | | | | | 8
--------------------------------------------
| | | | | | | | | | | | 9
--------------------------------------------
| | | | | | | | | | | | 10
--------------------------------------------
| | | | | | | | | | | | 11
--------------------------------------------
'''
That way you can then go in to the Python file and edit the letters individually with ease. The ingestion function is
def ingest(self, board_string):
'''A method to take the string representation
of the board and add it to the class variable self.letters'''
rows = [row for i, row in enumerate(board_string.split('\n')) if i % 2 and i != 1][:-1]
for index, row in enumerate(rows):
new_row = [letter for i, letter in enumerate(row) if i % 4 == 2][:-1]
new_row = ['' if letter == ' ' else letter for letter in new_row]
self.letters[:, 10 - index] = new_row
for i in range(11):
if new_row[i] != '':
self.powers[i, 10 - index] = ''
Finally, we want a method to print out the current state of the board, either the powers or the letters. (I decided to keep them on seperate boards because it just all looks a little cluttered otherwise)
def print_board(self, board_type='letters'):
'''A method to print out the board'''
print(" A B C D E F G H I J K ")
print(" " + '-' * 11 * 4)
if board_type == 'letters':
for y in reversed(range(11)):
for x in range(11):
item = str(self.letters[x, y])
if item == '':
item = ' '
print('| ' + item, end=" ", flush=True)
print('| {}'.format(11 - y), '\n', '-' * 11 * 4)
elif board_type == 'powers':
for y in reversed(range(11)):
for x in range(11):
item = str(self.powers[x, y])
if item == '':
item = ' '
print('|' + item, end="", flush=True)
print('| {}'.format(11 - y), '\n', '-' * 11 * 4)
1.3 A Basic Solver
The most basic way in which you might want to search for solutions can be posed like this: given a set of \(n\) letters, what possible words can we make from those? The way to solve this is simply to find every possible permutation of letters of length \(n\) or less, and check each one against the dictionary. Python has some lovely functionality built in for finding combinations and permutations in the itertools module for just this type of thing.
from itertools import permutations, combinations
def find_words_simple(letters):
'''Find every possible word for a given set of letters'''
all_combs = []
all_perms = []
for n in range(1, 8):
all_combs += [''.join(p) for p in combinations(letters, n)]
for comb in all_combs:
all_perms += [''.join(p) for p in permutations(comb)]
all_perms = set(all_perms)
all_words = []
for perm in all_perms:
if exists(perm):
all_words.append(perm)
return all_words
find_words_simple('jkros')
['kors', 'ors', 'or', 'os', 'kos', 'so', 'jo', 'kor']
Thus concludes part 1. Read on in part 2 to find out how to use the Board class in conjunction with a Solver class to find the best possible move on a board.